Theo khảo sát thực tế của cửa hàng chúng tôi cho thấy hiện thời có khôn cùng nhiều chúng ta học sinh không biết số bao gồm phương là gì? Hoặc không chứng minh được đấy là số bao gồm phương. Cũng chính vì vậy, trong nội dung bài viết dưới đây, Điện thứ Sharp việt nam sẽ share lý thuyết số chính phương là gì? Tính hóa học của số chính phương và những dạng bài tập số thiết yếu phương thường chạm mặt có lời giải chi tiết để các bạn cùng xem thêm nhé
Số bao gồm phương là gì?
Số bao gồm phương hay có cách gọi khác là số hình vuông vắn là số tự nhiên và thoải mái có căn bậc hai là một trong những tự nhiên hay có thể nói rằng số chủ yếu phương bằng bình phương (lũy quá bậc 2) của một trong những tự nhiên. Số bao gồm phương biểu lộ diện tích của một hình vuông có chiều lâu năm cạnh thông qua số tự nhiên.
Bạn đang xem: Số chính phương là j
Số chủ yếu phương bao gồm 2 dạng thiết yếu đó là:
Số chủ yếu phương chẵn là bình phương của một trong những chẵn. Ví dụ: 4, 16, 36… là số chính phương chẵn.Số bao gồm phương lẻ là bình phương của một số lẻ. Ví dụ: 9, 49, 81… là số bao gồm phương lẻ.Tính chất số chính phương
Tận cùng của số chính phương là 0, 1, 4, 5, 6, 9. Nếu những số tận thuộc là 2,3,7,8 thì không hẳn là số thiết yếu phương.Số thiết yếu phương chỉ tất cả thể có 1 trong 2 dạng: 4n hoặc 4n + 1, không tồn tại số thiết yếu phương nào có dang 4n + 2 hoặc 4n + 3 (với n € N).Số chủ yếu phương chỉ bao gồm thể có một trong 2 dạng: 3n hoặc 3n + 1, không tồn tại số bao gồm phương nào tất cả dạng 3n + 2 (với n € N).Khi so với ra quá số nguyên tố, số chính phương chỉ chứa những thừa số nguyên tố với số mũ chẵn.Số bao gồm phương tất cả chữ số tận cùng là một hoặc 9 thì chữ số hàng trăm là chữ số chẵn.Số chính phương tận cùng bởi 5 thì chữ số hàng trăm là 2.Số thiết yếu phương tận cùng bằng 4 thì chữ số hàng trăm là chữ số chẵn.Số thiết yếu phương tận cùng bằng 6 thì chữ số hàng trăm là chữ số lẻ.Số chủ yếu phương phân chia hết cho 2 thì phân chia hết đến 4.Số chủ yếu phương phân tách hết mang đến 3 thì phân chia hết mang lại 9.Số bao gồm phương phân tách hết cho 5 thì phân tách hết mang đến 25.Số bao gồm phương chia hết mang đến 8 thì phân tách hết mang đến 16.Số thiết yếu phương chia cho 3 không khi nào có số dư là 2; phân chia cho 4 không lúc nào dư 2 hoặc 3; số thiết yếu phương khi chia 8 luôn dư 0 hoặc 1 hoặc 4.Công thức để tính hiệu của nhị số chính phương: a2 – b2 = (a – b)(a + b).Số mong nguyên dương của số bao gồm phương là một vài lẻ.Số chủ yếu phương phân chia hết đến số nguyên tố phường thì chia hết mang đến p2.Tất cả các số thiết yếu phương rất có thể viết thành hàng tổng của các số lẻ tăng vọt từ 1: 1; 1 + 3; 1 + 3 + 5; 1 + 3 + 5 + 7; 1 + 3 + 5 + 7 + 9;…v.vCác dạng bài xích tập về số bao gồm phương
Dạng 1: minh chứng một số là số chủ yếu phương, hay những tổng nhiều số thiết yếu phương.
Phương pháp: Để chứng tỏ một số n là số là số bao gồm phương ta thường phụ thuộc vào định nghĩa, tức là chứng minh: n = k2 (k ∈ Z)
Ví dụ 1: minh chứng rằng những số nguyên x, y thì:
A = (x + y)(x + 2y)(x + 3y)(x + 4y) + y4 là số bao gồm phương.
Lời giải
Ta gồm A = (x + y)(x + 2y)(x + 3y)(x + 4y) + y4
= (x2 + 5xy + 4y2)(x2 + 5xy + 6y2) + y4
Đặt x2 + 5xy + 5y2 = t (t ∈ Z) thì
A = (t – y2)(t + y2) + y4 = t2 – y4 + y4 = t2 = (x2 + 5xy + 5y2)2
Vì x, y, z ∈ Z nên x2 ∈ Z, 5xy ∈ Z, 5y2 ∈ Z => (x2 + 5xy + 5y2) ∈ Z
Vậy A là số chủ yếu phương.
Ví dụ 2: mang đến B = 1.2.3 + 2.3.4 +…+ k k + 1 k + 2 cùng với k là số tự nhiên. Chứng tỏ rằng 4B + 1 là số chủ yếu phương
Lời giải:
Ta thấy biểu thức B là tổng của một biểu thức chúng ta nghĩ tới sự việc phải thu gọn biểu thức B trước
Ta có:
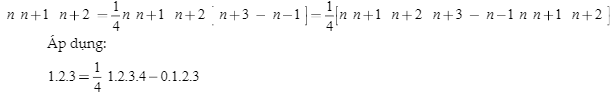
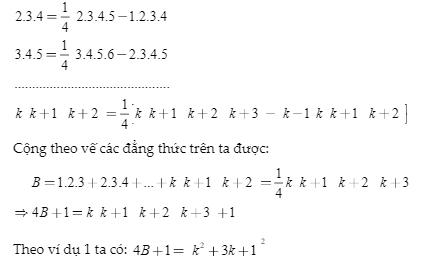
Vì k ∈ N bắt buộc k2 + 3k + 1 ∈ N. Vậy 4B + một là số chủ yếu phương
Ví dụ 3: chứng minh tích của 4 số từ nhiên tiếp tục cộng 1 luôn là số chính phương.
Xem thêm: Mát Mẻ Của Nữ Sinh Cấp 3 Hải Phòng, Điểm Báo Hằng Ngày Về Hải Phòng (Ngày 20/5/2021)
Giải:
Gọi 4 số tự nhiên, liên tục đó là n, n + 1, n + 2, n + 3 (n ∈ Z). Ta có:
n(n + 1)(n + 2)(n + 3) + 1 = n.( n + 3)(n + 1)(n + 2) + 1
= (n2 + 3n)(n2 + 3n + 2) + 1 (*)
Đặt n2 + 3n = t (t ∈ N) thì (*) = t(t + 2) + 1 = t2 + 2t + 1 = (t + 1)2
= (n2 + 3n + 1)2
Vì n ∈ N buộc phải n2 + 3n + 1 ∈ N. Vậy n(n + 1)(n + 2)(+ 3) + 1 là số bao gồm phương.
Dạng 2: Tìm quý hiếm của trở nên để biểu thức là số chủ yếu phương
Ví dụ 1:Tìm số tự nhiên và thoải mái n làm sao cho các số sau là số bao gồm phương
a) n2 + 2n + 12
b) n(n + 3)
c) 13n + 3
d) n2 + n + 1589
Lời giải:
a) bởi n2 + 2n + 12 là số chính phương nên được đặt n2 + 2n + 12 = k2 (k ∊ N)
(n2 + 2n + 1) + 11 = k2
⇔ k2 – (n + 1)2 = 11
⇔ (k + n + 1)(k – n – 1) = 11
Nhận xét thấy k + n + 1 > k – n – 1 và bọn chúng là hồ hết số nguyên dương, buộc phải ta có thể viết
(k + n + 1) (k – n – 1) = 11.1
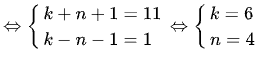
b) Đặt n(n + 3) = a2 (n ∊ N)
⇒ n2 + 3n = a2
⇔ 4n2 + 12n = 4a2
⇔ (4n2 + 12n + 9) – 9 = 4a2
⇔ (2n + 3)2 – 4a2 = 9
⇔ (2n + 3 + 2a).(2n + 3 – 2a) = 9
Nhận xét thấy 2n + 3 + 2a > 2n + 3 – 2a và bọn chúng là đều số nguyên dương, yêu cầu ta hoàn toàn có thể viết (2n + 3 + 2a)(2n + 3 – 2a) = 9.1
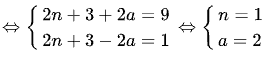
c) Đặt 13n + 3 = y2 (y ∊ N)
⇒ 13(n – 1) = y2 – 16
⇔ 13(n – 1) = (y + 4)(y – 4)
⇒ (y + 4)(y – 4) chia hết cho 13 nhưng 13 là số nguyên tố bắt buộc y + 4 chia hết mang lại 13 hoặc y – 4 phân tách hết đến 13
⇒ y = 13k ± 4 (với k ∊ N)
⇒ 13(n – 1) = (13k ± 4)2 – 16 = 13k.(13k ± 8) = 13k2 ± 8k + 1
Vậy n = 13k2 ± 8k + 1 (với k ∊ N) thì 13n + 3 là số chủ yếu phương
d) Đặt n2 + n + 1589 = m2 (m ∊ N)
⇒ (4n2 + 1)2 + 6355 = 4m2
⇔ (2m + 2n + 1) (2m – 2n – 1) = 6355
Nhận xét thấy 2m + 2n + 1 > 2m – 2n – 1 > 0 và bọn chúng là hầu như số lẻ, bắt buộc ta rất có thể viết
(2m + 2n + 1) (2m – 2n – 1) = 6355.1 = 1271.5 = 205.31 = 155.41
Suy ra n có thể có những giá trị sau : 1588 ; 316 ; 43 ; 28
Dạng 3: tra cứu số bao gồm phương
Ví dụ : A là số thiết yếu phương gồm gồm 4 chữ số. Phân phối mỗi chữ số của A một đối kháng vị, ta vẫn được một trong những chính phương B. Yêu thương cầu: Hãy kiếm tìm A với B.
Lời giải
Dạng 4: chứng tỏ một số không phải là số chủ yếu phương
Ví dụ: chứng minh số 1234567890 không phải là số chủ yếu phương.
Giải:
Số 1234567890 chia hết cho 5 (vì chữ số tận thuộc là 0) dẫu vậy không phân chia hết mang lại 25 (vì nhị chữ số tận cùng là 90).
Do đó số 1234567890 không hẳn là số bao gồm phương.
Hy vọng cùng với những kiến thức và kỹ năng về số chính phương là gì và đặc thù số chủ yếu phương rất có thể giúp các bạn áp dụng vào làm bài tập. Kế bên ra, các chúng ta có thể tham khảo cấp cho số cộng là gì? công thức cấp số cộng và bài xích tập có lời giải tại: https://quartetpress.com/tu-van-dich-vu/cap-so-cong/
