Nếu như ở lớp 10 các em đã biết cách tính khoảng cách giữa 2 điểm, từ điểm tới đường thẳng hay giữa hai đường thẳng song song trong mặt phẳng, thì ở lớp 11 với phần hình học không gian chúng ta sẽ làm quen với khái niệm 2 đường thẳng chéo nhau và cách tính khoảng cách giữa chúng.
Bạn đang xem: Tính khoảng cách giữa 2 đường thẳng
Việc tính khoảng cách giữa 2 đường thẳng chéo nhau trong không gian chắc chắn sẽ gây chút khó khăn với nhiều bạn, bởi hình học không gian có thể nói "khó nhằn" hơn trong mặt phẳng.
Tuy nhiên, các bạn cũng đừng quá lo lắng, bài viết dưới đây chúng ta sẽ cùng nhau ôn lại các phương pháp tính khoảng cách giữa 2 đường thẳng chéo nhau trong không gian, và vận dụng giải các bài tập minh họa.
1. Hai đường thẳng chéo nhau - kiến thức cần nhớ
- Hai đường thẳng được gọi là chéo nhau trong không gian khi chúng không cùng một mặt phẳng, không song song và không cắt nhau.
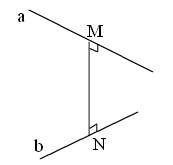
• Khoảng cách giữa 2 đường thẳng chéo nhau là độ dài đoạn vuông góc chung của 2 đường thẳng đó.
Ký hiệu: d(a;b) = MN trong đó M ∈ a, N ∈ b và MN ⊥ a; MN ⊥ b;
• Khoảng cách giữa hai đường thẳng chéo nhau bằng khoảng cách giữa một trong hai đường thẳng đó và mặt phẳng song song với nó mà chứa đường thẳng còn lại.
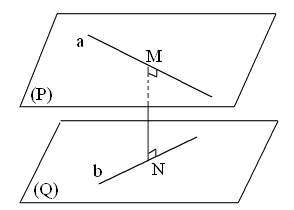
Ký hiệu: d(a,b) = d(a,(Q)) = d(b,(P)) = d((P),(Q)) trong đó (P), (Q) là hai mặt phẳng lần lượt chứa các đường thẳng a, b và (P)//(Q).
2. Cách tính khoảng cách giữa 2 đường thẳng chéo nhau
- Để tính khoảng cách giữa 2 đường thẳng chéo nhau tùy vào đề bài toán ta có thể dùng một trong các phương pháp sau:
* Phương pháp 1: Dựng đoạn vuông góc chung IJ của a và b, tính độ dài đoạn IJ, khi đó d(a,b) = IJ.
¤ Ta xét 2 trường hợp sau:
• TH1: Hai đường thẳng Δ và Δ" chéo nhau và vuông góc với nhau
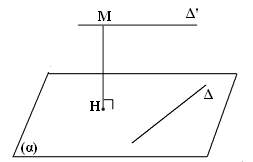
+ Bước 1: Chọn mặt phẳng (α) chứa Δ" và vuông góc với Δ tại I.
+ Bước 2: Trong mặt phẳng (α) kẻ IJ ⊥ Δ".
- Khi đó IJ là đoạn vuông góc chung của 2 đường thẳng Δ và Δ", và d(Δ,Δ") = IJ.
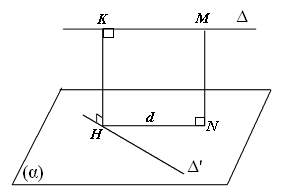
• TH2: Hai đường thẳng Δ và Δ" chéo nhau và KHÔNG vuông góc với nhau
- Ta dựng đoạn vuông góc chung của hai đường thẳng Δ và Δ" theo một trong 2 cách sau:
° Cách 1:
+ Bước 1: Chọn mặt phẳng (α) chứa Δ" và song song với Δ.
+ Bước 2: Dụng d là hình chiếu vuông góc của Δ xuống (α) bằng cách lấy điểm M ∈ Δ dựng đoạn MN ⊥ (α), lúc đó d là đường thẳng đi qua N và song song với Δ.
+ Bước 3: Gọi H = d ∩ Δ", dụng HK//MN.
Khi đó HK là đoạn vuông góc chung của Δ và Δ", và d(Δ,Δ") = HK = MN.
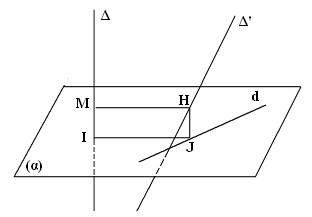
° Cách 2:
+ Bước 1: Chọn mặt phẳng (α) ⊥ Δ tại I.
+ Bước 2: Tìm hình chiếu d của Δ" xuống mặt phẳng (α).
+ Bước 3: Trong mặt phẳng (α), dụng IJ ⊥ d, từ J dựng đường thẳng song song với Δ và cắt Δ" tại H, từ H dựng HM//IJ.
Khi đó HM là đoạn vuông góc chung của 2 đường thẳng Δ và Δ", và d(Δ,Δ") = HM =IJ.
* Phương pháp 2: Chọn mặt phẳng (α) chứa đường thẳng Δ và song song với Δ", khi đó: d(Δ,Δ") = d(Δ,(α)).
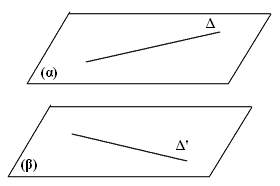
* Phương pháp 3: Dựng 2 mặt phẳng song song (α), (β) và lần lượt chứa 2 đường thẳng Δ và Δ". Khi đó, khoảng cách giữa 2 mặt phẳng là khoảng cách của 2 đường thẳng cần tìm.
3. Bài tập vận dụng cách tính khoảng cách giữa 2 đường thẳng chéo nhau. Xem thêm: Địa Điểm Lịch Sử Ở Việt Nam Qua Năm Tháng, Di Tích Lịch Sử
* Ví dụ 1: Cho hình lập phương ABCD.A"B"C"D" cạnh bằng a. Xác định đoạn vuông chung và tính khoảng cách giữa 2 đường thẳng AD" và A"B"?
* Lời giải:
- Ta có hình minh họa như sau:
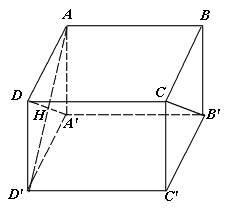
- Gọi H là giao điểm của AD" với A"D. Vì ADD"A" là hình vuông nên A"H ⊥ AD".
- Ta có: A"H ⊥ AD" và A"H ⊥ A"B" ⇒ AH" là đoạn vuông góc chung của 2 đường thẳng AD" và A"B".
d(A"B";AD") = A"H = a√2/2.
* Ví dụ 2: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a và SA ⊥ (ABCD). Biết mặt phẳng (SBC) tạo với đáy một góc 600.
a) Tính khoảng cách giữa 2 đường thẳng SB và CD.
b) Tính khoảng cách giữa 2 đường thẳng BD và SC.
* Lời giải:
- Minh họa như hình vẽ sau:
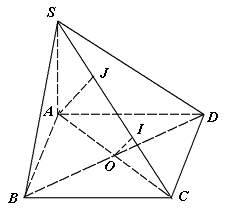
a) Theo giải thiết, ta có: BC ⊥ AB và BC ⊥ SA nên ⇒ BC ⊥ (SAB) ⇒ BC ⊥ SB
- Lại có: BC ⊥ CD (ABCD vuông)
⇒ BC là đoạn vuông góc chung của SB và CD
- Ta có: d(SB;CD) = BC = a.
b) Theo câu a) ta có: BC ⊥ (SAB)
Do đó:
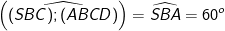
⇒ SA = AB.tan600 = a√3.
- Gọi O là tâm hình vuông ABCD, ta có: BD ⊥ AC và BD ⊥ SA ⇒ BD ⊥ (SAC).
- Kẻ OI ⊥ SC khi đó OI là đường vuông góc chung của SC và BD, ta có:
ΔCAS ∼ ΔCOI (theo g-g)
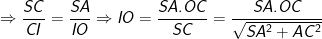
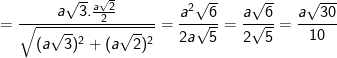
+ Cách khác: cũng có thể dựng AJ ⊥ SC ⇒ OI = (1/2)AJ
Mặt khác:
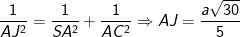
suy ra:
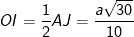
* Ví dụ 3: Cho hình chóp SABC có SA = 2a và vuông góc với mặt phẳng (ABC), đáy ABC là tam giác vuông cân tại B với AB = a. Gọi M là trung điểm của AC. Hãy dựng và tính đoạn vuông góc chung của SM và BC.
* Lời giải:
- Minh họa như hình vẽ sau:
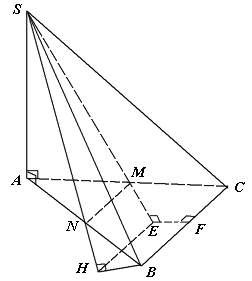
° Dựng đoạn vuông góc chung của SM và BC ta có thể thực hiện 1 trong 2 cách sau:
* Cách 1: Gọi N là trung điểm của AB, NM//BC ⇒ BC//(SMN).
- Ta có: MN ⊥ AB và MN ⊥ SA ⇒ MN ⊥ (SAB) ⇒ (SMN) ⊥ (SAB).
Mà (SMN) ∩ (SAB) = SN, hạ BH ⊥ (SMN)
Từ H dụng Hx // BC và cắt SM tại E. Từ E dựng Ey // BH và cắt BC tại F.
⇒ Đoạn EF là đoạn vuông gó chung của SM và BC.
* Cách 2: Ta thấy: BC ⊥ AB và BC ⊥ SA nên suy ra BC ⊥ (SAB).
Suy ra (SAB) là mp qua B thuộc BC và vuông góc với BC
Gọi N là trung điểm của AB ⇒ MN // BC ⇒ MN ⊥ (SAB).
⇒ MN là hình chiếu vuông góc của SM lên (SAB).
Hạ BH ⊥ SN ⇒ BH ⊥ (SMN)
Từ H dụng Hx // BC và cắt SM tại E. Từ E dựng Ey // BH và cắt BC tại F.
⇒ Đoạn EF là đoạn vuông gó chung của SM và BC.
° Tính EF (đoạn vuông gó chung của SM và BC)
- Ta thấy ΔSAN và ΔBHN là 2 tam giác vuông có 2 góc nhọn đối đỉnh
⇒ ΔSAN ∼ ΔBHN (g-g)
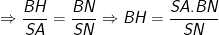
- Trong đó:
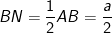
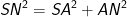
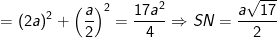
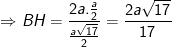
- Vậy khoảng cách giữa SM và BC là BH bằng: 2a(√17/17).
* Ví dụ 4: Cho hình chóp S.ABCD có SA ⊥ (ABCD), đáy ABCD là hình chữ nhật với AC = a√5 và BC = a√2. Tính khoảng cách giữa 2 đường thẳng chéo nhau SD và BC.
* Lời giải: (Bài toán này ta vận dụng phương pháp 2 để giải)
- Minh họa như hình vẽ sau:
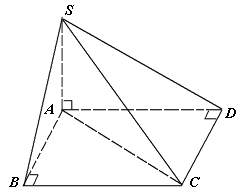
- Theo giả thiết, ta có: BC//AD nên BC//(SAD)
⇒ d(BC;SD) = d(BC; (SAD)) = d(B;(SAD))
- Mặt khác: AB ⊥ AD và AB ⊥ SA ⇒ AB ⊥ (SAD) ⇒ d(B;SAD) = AB.
- Lại có:
- Vậy khoảng cách giữa hai đường thẳng chéo nhau SD và BC là AB bằng a√3.
* Ví dụ 5: Cho hình hộp chữ nhật ABCD.A"B"C"D" có AB = 3; AD = 4; AA" = 5. Tính khoảng cách giữa 2 đường thẳng chéo nhau AC và B"D"?















