Giới hạn của hàm số, cách tính và bài tập áp dụngGiới hạn hữu hạnTính giới hạn của dãy sốCÁCH TÍNH GIỚI HẠN HÀM SỐ NHƯ THẾ NÀO?

Giới hạn của hàm số, cách tính và bài tập áp dụng

Giới hạn hữu hạn

*
*
Giới hạn vô cực, Giới hạn ở vô cực
*
*
*
Giới hạn 1 bên
*
*

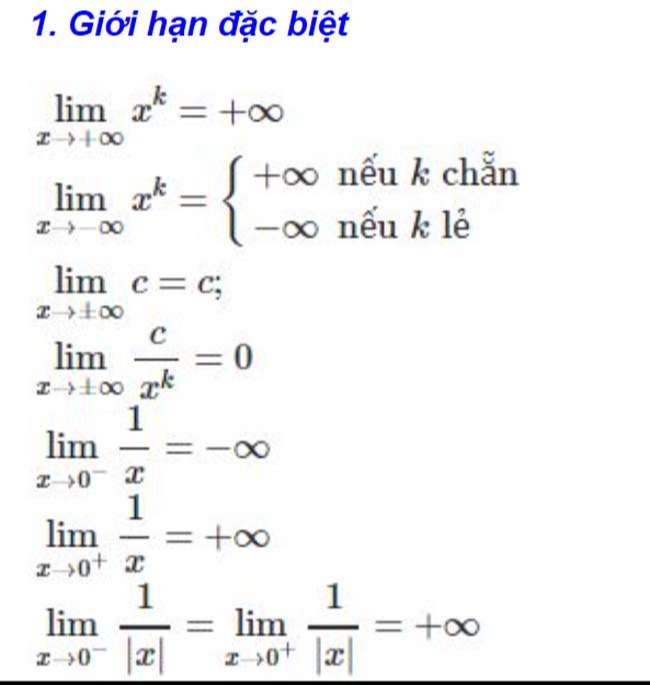
Bài tập áp dụng tìm giới hạn

*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*

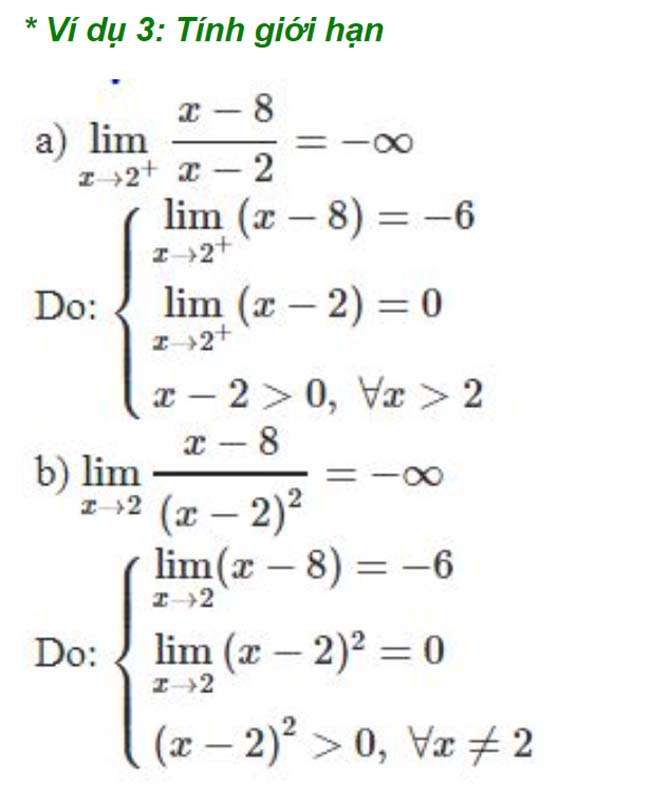
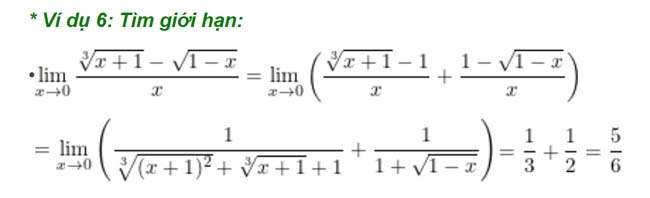
Ví dụ 8: Tìm giới hạn sau

*
*
*
*
*
*
*
*
*
*
*

Mối quan hệ giữa giới hạn một bên và giới hạn tại một điểm

*
*
*
*

Bảng các công thức tính giới hạn hàm số

Một số phương pháp tính lim thủ công

Tính giới hạn của dãy số

Cách 1:Sử dụng định nghĩa tìm giới hạn 0 của dãy số

*

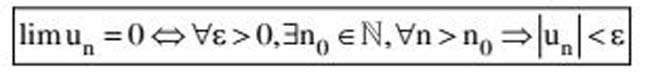
Cách 2:Tìm giới hạn của dãy số bằng công thức

Một số công thức ta thường gặp khi tính giới hạn hàm số như sau:

*

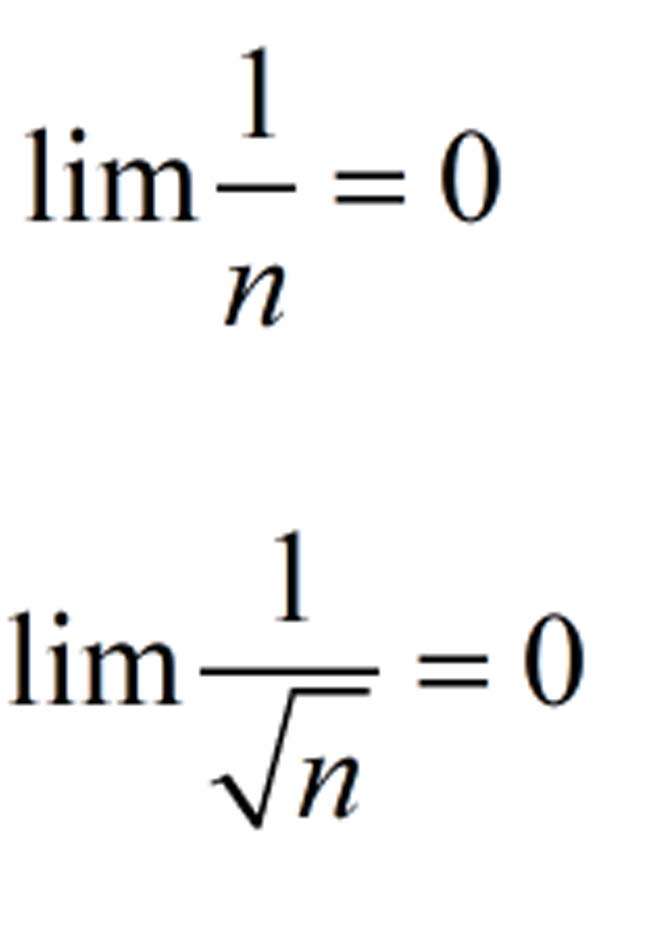
Công thức trên có thể biến tấu thành các dạng khác tuy nhiên về bản chất thì không thay đổi.

Bạn đang xem: Cách tính lim bằng tay

Cách 3:Sử dụng định nghĩa tìm giới hạn hữu hạn

*

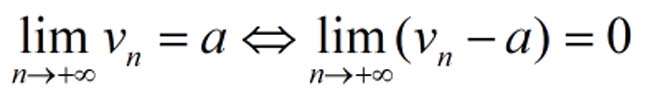
Cách 4:Sử dụng các giới hạn đặc biệt cùng với định lý để giải quyết các bài toán tìm giới hạn dãy số

Ta thường sử dụng các dạng giới hạn: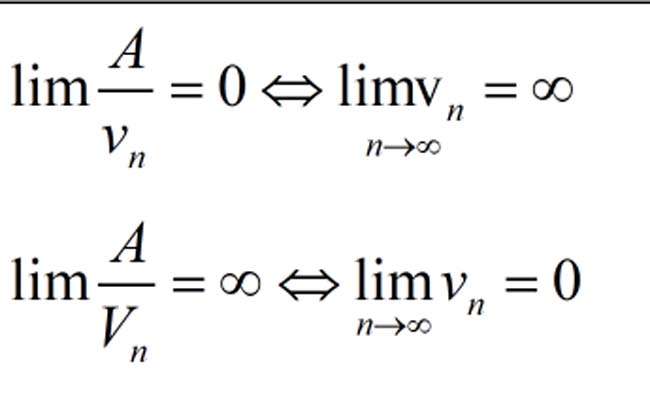
*
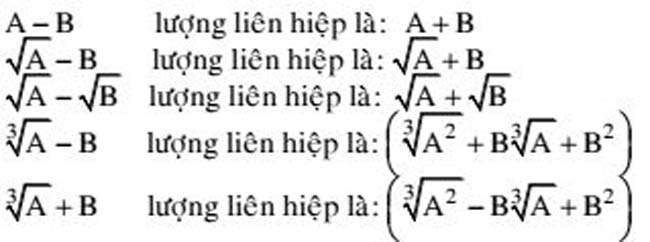
Nếu biểu thức có dạng phân thức tử số và mẫu số chứa lũy thừa của n thì ta tiến hành chia cả tử và mẫu cho n^k với k là mũ cao nhất ở bậc mẫu.Nếu biểu thức chứa căn thức cần nhân một lượng liên hợp để đưa về dạng cơ bản thì ta có một số lượng liên hợp cần thiết như sau:
*

Cách 5: Áp dụng công thức tính tổng cấp số nhân lùi vô hạn, tính giới hạn, biểu thị một số thập phân vô hạn tuần hoàn thành phân số.

Cấp số nhân lùi vô hạn là cấp số nhân vô hạn và có công bội là |q| Tổng các số hạng của một cấp số nhân lùi vô hạn (Un)

S = u1 + u2 + u3 + u4 + …. + un = u1 / ( 1 – q )

Mọi số thập phân đều được biểu thị dưới dạng lũy thừa của 10.

Câu 6:Tìm giới hạn vô cùng của một dãy số bằng định nghĩa

*

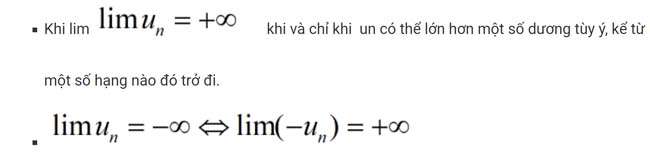
Cách 7:Tìm giới hạn của một dày số bằng cách sử dụng định lý, quy tắc tìm giới hạn vô cực

Chứng minh một dãy số có giới hạn

Áp dụng định lý Vâyơstraxơ:

Nếu dãy số (un) tăng và bị chặn trên thì nó có giới hạn.Nếu dãy số (un) giảm và bị chặn dưới thì nó có giới hạn.

Chứng minh tính tăng và tính bị chặn:

Chứng minh một dãy số tăng và bị chặn trên (dãy số tăng và bị chặn dưới) bởi số M ta thựchiện: Tính một vài sốhạng đầu tiên của dãy và quan sát mối liên hệ để dự đoán chiều tăng(chiều giảm) và số M.

Tính giới hạn của dãy số ta thực hiện theo một trong hai phương pháp sau:

Phương pháp 1

Đặt lim un = a. Từ lim u(n+1) = lim f(un) ta được một phương trình theo ẩn a.

Giải phương trình tìm nghiệm a và giới hạn của dãy (un) là một trong các nghiệm củaphương rình. Nếu phương trình có nghiệm duy nhất thì đó chính là giới hạn cảu dãy cầntìm. còn nếu phương trình có nhiều hơn một nghiệm thì dựa vào tính chất của dãy số đểloại nghiệm.

Chú ý:Giới hạn của dãy số nếu có là duy nhất.

Phương pháp 2:Tìm công thức tổng quát un của dãy số bằng cách dự đoán. Chứng minh công thức tổng quát un bằng phương pháp quy nạp toán học.Tính giới hạn của dãy thông qua công thức tổng quát đó.

Tính giới hạn của hàm số

Để tính giới hạn của hàm số ta có thể thực hiện một số phương pháp như sau:

Dùng định nghĩa để tìm giới hạnTìm giới hạn của hàm số bằng công thứcSử dụng định nghĩa tìm giới hạn một bênSử dụng định lí và công thức tìm giới hạn một bênTính giới hạn vô cựcTìm giới hạn của hàm số dạng 0/0Dạng vô định

Dưới đây là một số công thức tính hàm số vô cùng cơ bản:

*

Cách tính lim bằng máy tính

Bước 1: Trước tiên hãy nhập biểu thức vào máy tính

Bước 2: Sử dụng chức năng đó là gán số tính giá trị biểu thức

Bước 3: Lưu ý gán các giá trị theo bên dưới:

+) Lim về vô cùng dương thì hãy gán số 100000

+) Lim về vô cùng âm thì hãy gán số -100000

+) Lim về 0 thì hãy gán số 0.00000001

+) Lim về số bất kì chẳng hạn như về +3 thì gán 3.000000001 còn về 3- thì gán 2.9999999999

Tính lim là một dạng bài tập khá cơ bản, tuy nhiên dạng toán này vẫn chiếm một vài câu trong đề thi trung học phổ thông quốc gia. Các bạn cần đảm bảo tính chính xác khi làm. Đặc biệt có thể sử dụng máy tính Casio để có thể tính toán nhanh và chính xác nhất.

Chuyên đề giới hạn và liên tục

CÁCH TÍNH GIỚI HẠN HÀM SỐ NHƯ THẾ NÀO?

TÍNH GIỚI HẠN HÀM SỐ DẠNG XÁC ĐỊNH

Nếu hàm f(x) xác định tại điểm lấy giới hạn. Thì ta chỉ việc thay điểm đó vào biểu thức dưới dấu lim sẽ được kết quả cần tìm.

*

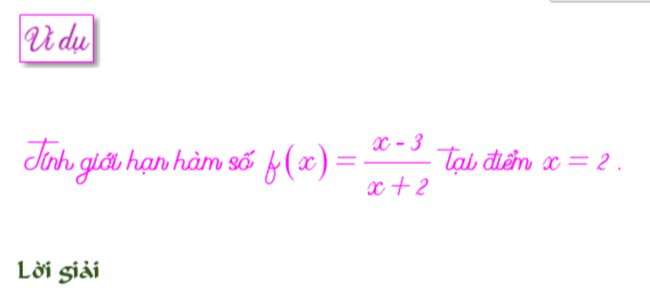
Ta chỉ việc thay x=2 vào biểu thức trong dấulimta được-1/4. Và đó chính là kết quả của giới hạn trên.

TÌM GIỚI HẠN HÀM SỐ DẠNG BẤT ĐỊNH

Đối với dạng bất định ta quan tâm tới một số dạng thường gặp như sau:

1. TÌM GIỚI HẠN CỦA HÀM SỐ DẠNG 0 TRÊN 0

Đối với dạng 0 trên 0 ta lại chia làm 2 loại: Loại giới hạnkhông chứa cănvà loạichứa căn.

Xem thêm: Đọc Truyện One Piece - Truyện Tranh One Piece

Loạikhông chứa cănbao gồm các loại giới hạn đặc biệt và loại phân thức mà tử và mẫu là các đa thức.

Giới hạn đặc biệt dạng 0 trên 0 được đề cập đến trong chương trình phổ thông hiện nay là:

*

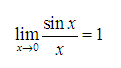
Cách tính giới hạndạng 0 trên 0loại đa thức trên đa thứcthì ta phân tích thành nhân tử bằng lược đồ Hoocner.

*

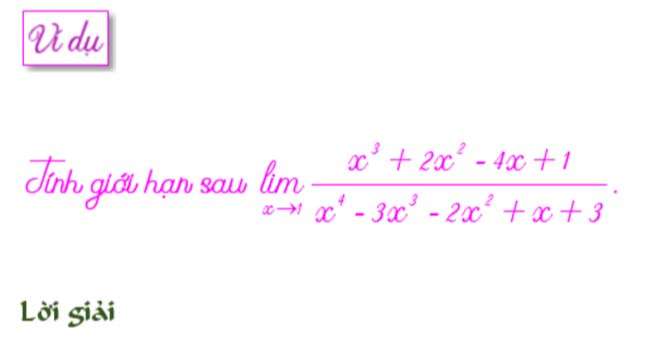
Ta thấy x=1 là nghiệm của cả tử số và mẫu số. Ta dùng lược đồ Hoocner để phân tích tử số và mẫu số.

*

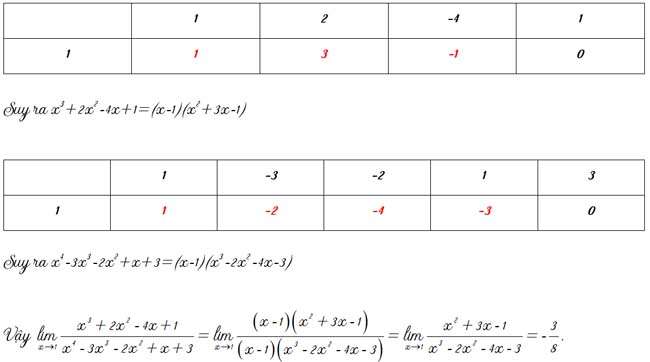
Còn để tính loại chứa căn ta thực hiện nhân cả tử và mẫu với biểu thức liên hợp.

*
*

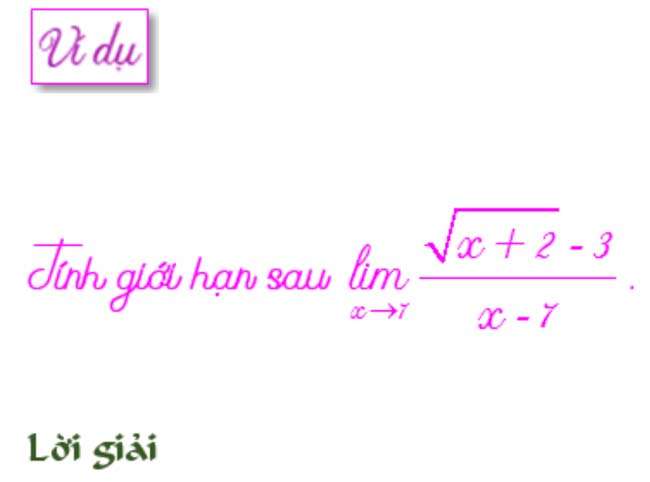
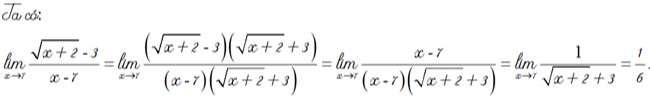
Với căn bậc 3 ta cũng làm tương tự.

*

Ta có:

*

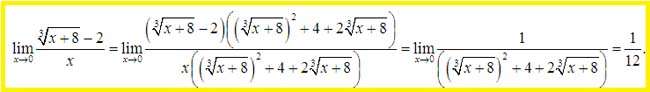
Trong trường hợp giới hạncó cả căn bậc 2 và căn bậc 3thì ta thêm bớt 1 lượng để đưa về tổng hiệu của 2 giới hạn dạng 0 trên 0.

*
*
GIỚI HẠN DẠNG VÔ CÙNG TRÊN VÔ CÙNG

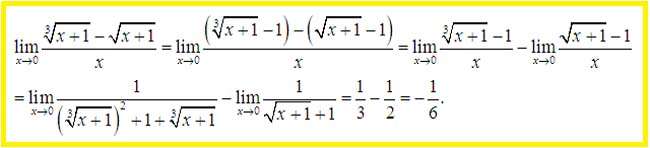
Với dạng giới hạn vô cùng trên vô cùng ta giải bằng cách chia cả tử và mẫu cho x với số mũ cao nhất của tử hoặc của mẫu. Lưu ý dạng này khi x tiến tới âm vô cùng chúng ta hay nhầm lẫn về dấu. Cụ thể khi đưa x vào trong căn bậc 2 ta cần để dấu – bên ngoài.

*
*
GIỚI HẠN DẠNG VÔ CÙNG TRỪ VÔ CÙNG

Với dạng vô cùng trừ vô cùng (vô cực trừ vô cực) ta thực hiện theo 2 phương pháp: Nhóm ẩn bậc cao nhất hoặc nhân liên hợp. Cách nào thuận lợi hơn ta tiến hành theo cách đó.

*

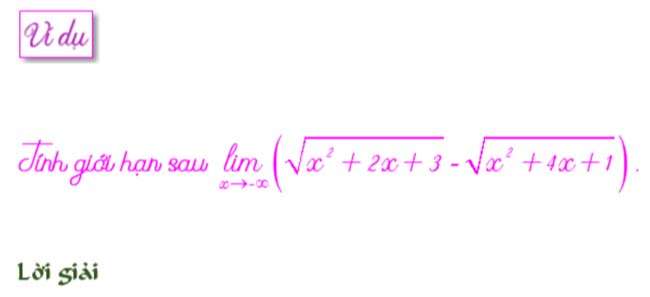
Trường hợp này chúng ta cầnnhân liên hợpbởi vì nếu nhóm x thì sẽ lại đưa về dạng bất định 0 nhân vô cùng.

*
*

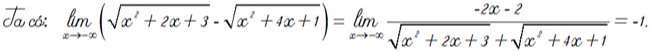
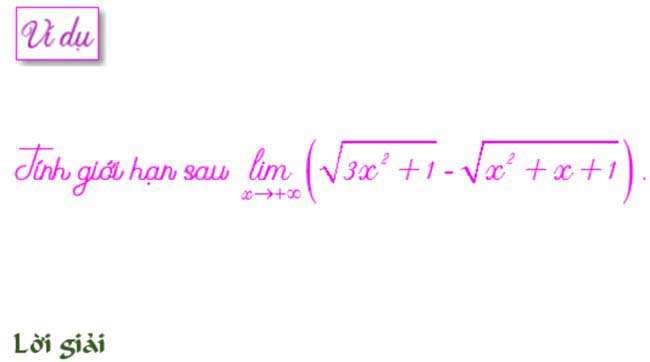
Bài này giống bài trên đều là dạng vô cùng trừ vô cùng. Nhưng ta lại để ý là hệ số bậc cao nhất trong 2 căn là khác nhau. Vì vậy bài này chúng ta nên nhóm nhân tử chung.

*
GIỚI HẠN DẠNG 1 MŨ VÔ CÙNG

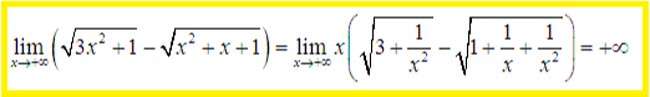
Với giới hạn dạng 1 mũ vô cùng ta tính thông qua giới hạn đặc biệt sau:

*
*
GIỚI HẠN DẠNG 0 NHÂN VÔ CÙNG

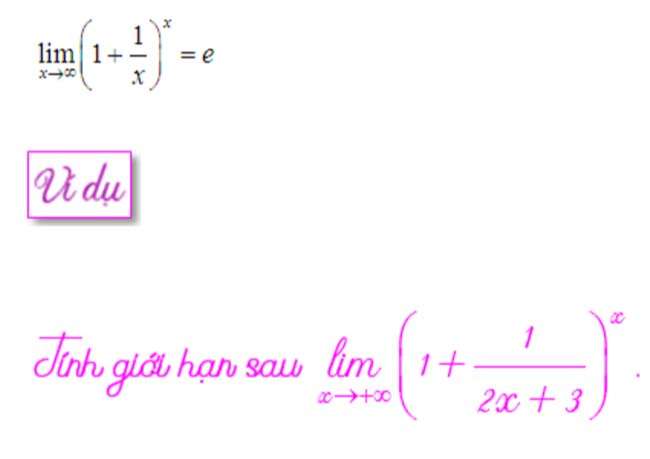
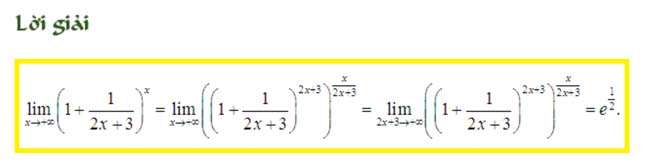
Về bản chất giới hạn dạng 0 nhân vô cùng có thể đưa về dạng 0 trên 0 hoặc dạng vô cùng trên vô cùng qua 1 vài phép biến đổi theo lưu ý ở đầu bài viết này phần định nghĩa. Với dạng giới hạn này chúng ta nên biến đổi về dạng xác định hoặc các dạng giới hạn vô định đã nêu ra ở trên. Tùy từng bài cụ thể chúng ta cần biến đổi cho phù hợp.

*
*

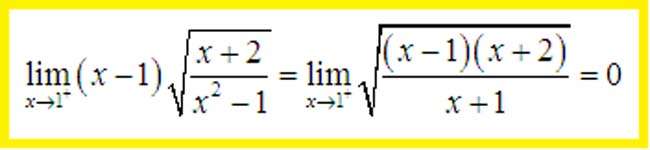
Phân dạng và các phương pháp giải toán chuyên đề giới hạn

BÀI 1. GIỚI HẠN CỦA DÃY SỐ.Dạng 1. Sử dụng định nghĩa tìm giới hạn 0 của dãy sốDạng 2. Sử dụng định lí để tìm giới hạn 0 của dãy sốDạng 3. Sử dụng các giới hạn đặc biệt và các định lý để giải các bài toán tìm giới hạn dãyDạng 4. Sử dụng công thức tính tổng của một cấp số nhân lùi vô hạn, tìm giới hạn, biểu thị một số thập phânvô hạn tuần hoàn thành phân sốDạng 5. Tìm giới hạn vô cùng của một dãy bằng định nghĩaDạng 6. Tìm giới hạn của một dãy bằng cách sử dụng định lý, quy tắc tìm giới hạn vô cựcMỘT SỐ DẠNG TOÁN NÂNG CAO {Tham khảo}BÀI 2. GIỚI HẠN HÀM SỐDạng 1. Dùng định nghĩa để tìm giới hạnDạng 2. Tìm giới hạn của hàm số bằng công thứcDạng 3. Sử dụng định nghĩa tìm giới hạn một bênDạng 4. Sử dụng định lý và công thức tìm giới hạn một bênDạng 5. Tính giới hạn vô cựcDạng 6. Tìm giới hạn của hàm số thuộc dạng vô định 0/0Dạng 7. Dạng vô địnhDạng 8. Dạng vô địnhMỘT SỐ DẠNG TOÁN NÂNG CAO {Tham khảo}BÀI 3. HÀM SỐ LIÊN TỤCDạng 1. Xét tính liên tục của hàm số f(x) tại điểm x0Dạng 2. Xét tính liên tục của hàm số tại một điểmDạng 3. Xét tính liên tục của hàm số trên một khoảng KDạng 4. Tìm điểm gián đoạn của hàm số f(x)Dạng 5. Chứng minh phương trình f(x)=0 có nghiệmMỘT SỐ BÀI TẬP LÝ THUYẾT {Tham khảo}